In this new post from the sftraj series, we now
present a detailed conceptual model for movement, from the basic
location to a complete trajectory. Essentially, this is the logics
behind sftraj.

What is a trajectory?
Movement can be described by the (continuous) curve made by moving objects. In practice, this curve is sampled (recorded) at discrete times to collect locations, which define tracking data of the form $(x, y, z, t)$, i.e. vertices composed of 2- or 3-dimensional spatial coordinates plus the temporal coordinate. A track or path is thus composed of a series of locations, i.e. the “complete spatio-temporal record of a followed organism, from the beginning to the end of observations”1.
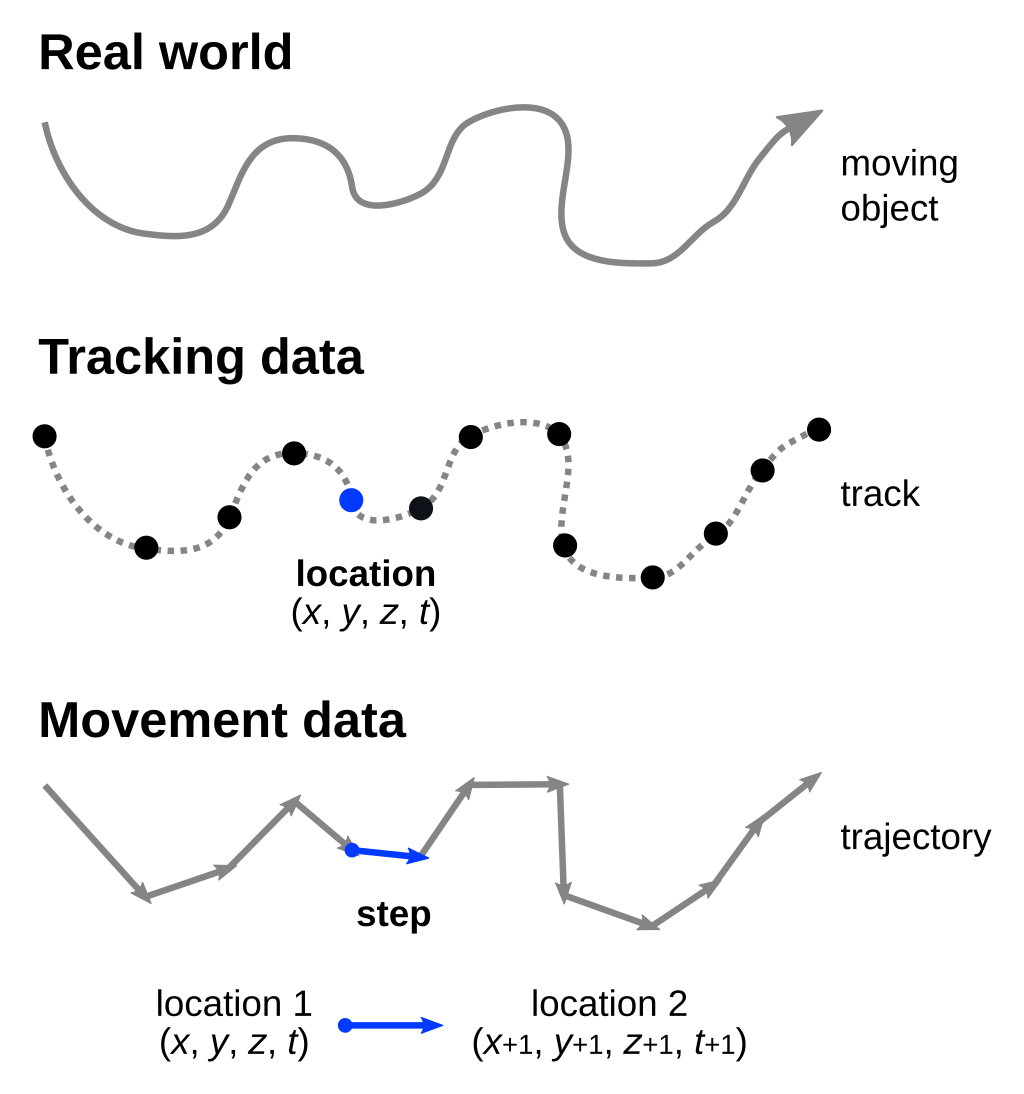
Considering the temporal autocorrelation between successive locations as part of the movement information2, we can then defines steps as the straight-line segments between two successive locations. Treating movement steps as straight lines is an “idealization” and the most parsimonious approach (other complex approaches exist in some fields, such as splines and Bezier curves), but at sufficient resolution, no significant information is lost. A sequence of steps finally forms a trajectory.
Movement is thus recorded by a series of locations in a track, and is abstracted as sequential steps in a trajectory. It is important to recognize this dual perspective between tracking data (locations) and movement data (steps).
A conceptual model for movement
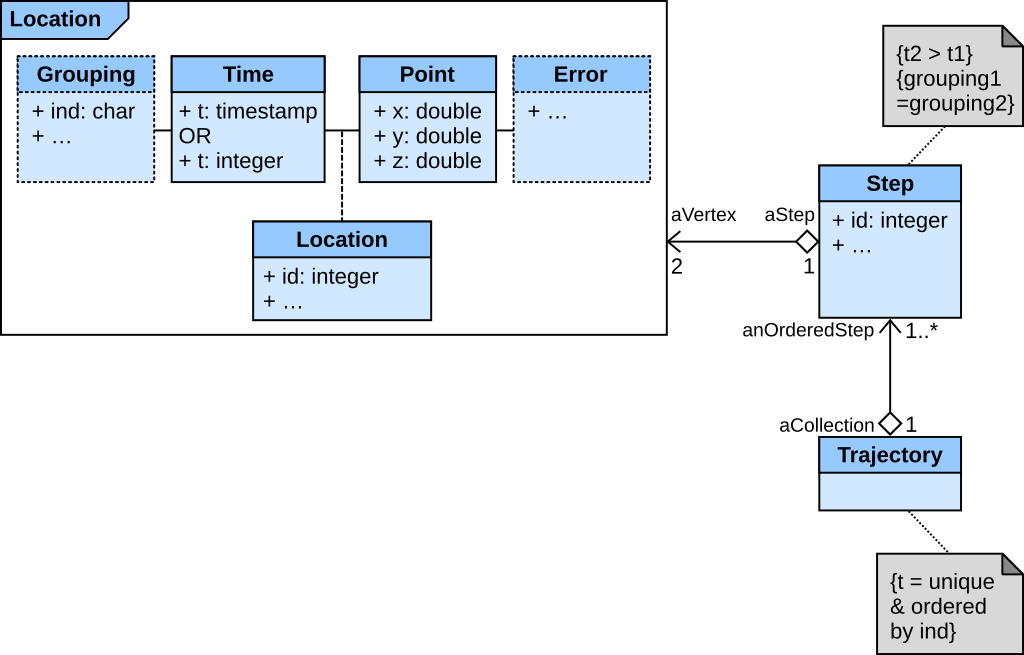
To organize these elements of data and how they relate to one another and to properties of the real world entities (here a moving object), we followed the methodology for conceptual modeling of geographic information that is specified in the International Standards (ISO/TC 211), which relies on a standard conceptual model specified in Unified Modeling Language (UML)3.
Locations
The basic element of the movement model is a location. A location is, in its simplest form, a point defined by its spatial coordinates $(x, y, z, t)$, with $z$ being optional, associated to the corresponding timestamp $t$ (note that the time can also be a simple integer defining the order, for instance in the case of a track in the snow). This is the raw data of movement, which is usually directly provided by a tracking device.
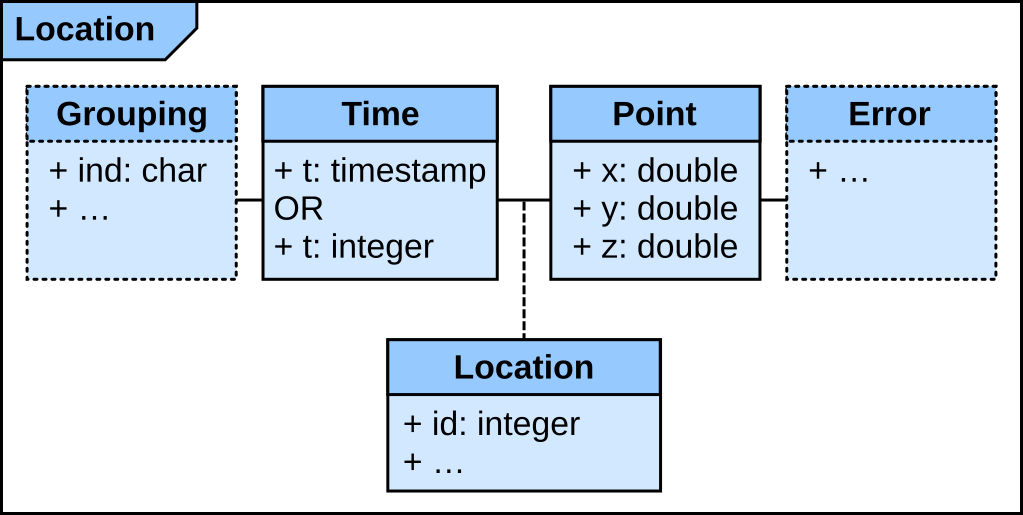
Additionally, “grouping” information can be provided for the location: this needs to be a minima the individual (‘ind’), e.g. the actual moving object (for instance an animal), but can also be extended to other hierarchical level of the data, such as the year, the burst, the movement behavior, etc.
Spatial points are never exact and can be characterized by an error. Typically, GPS and Argos data will provide information on the quality of the location, such as satellite data or dilution of precision (for GPS data). The challenge with this information on the error is the complete lack of standardization — as such, this will be left open for the time being.
Finally, a location can also include any information at the level of the point, such as environmental data measured at the location (e.g. land cover).
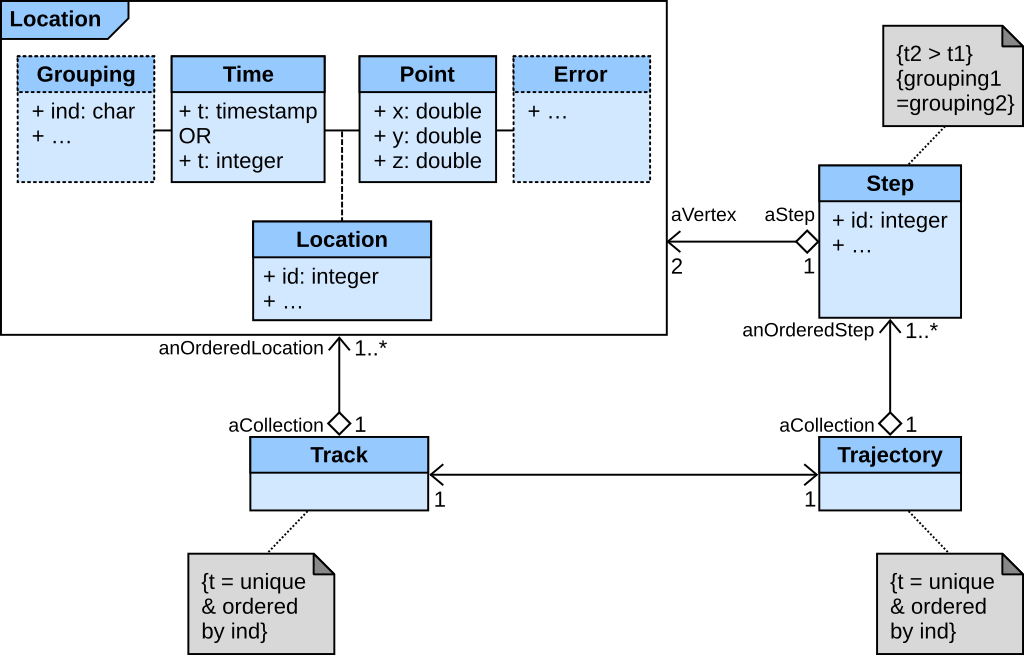
Tracking data
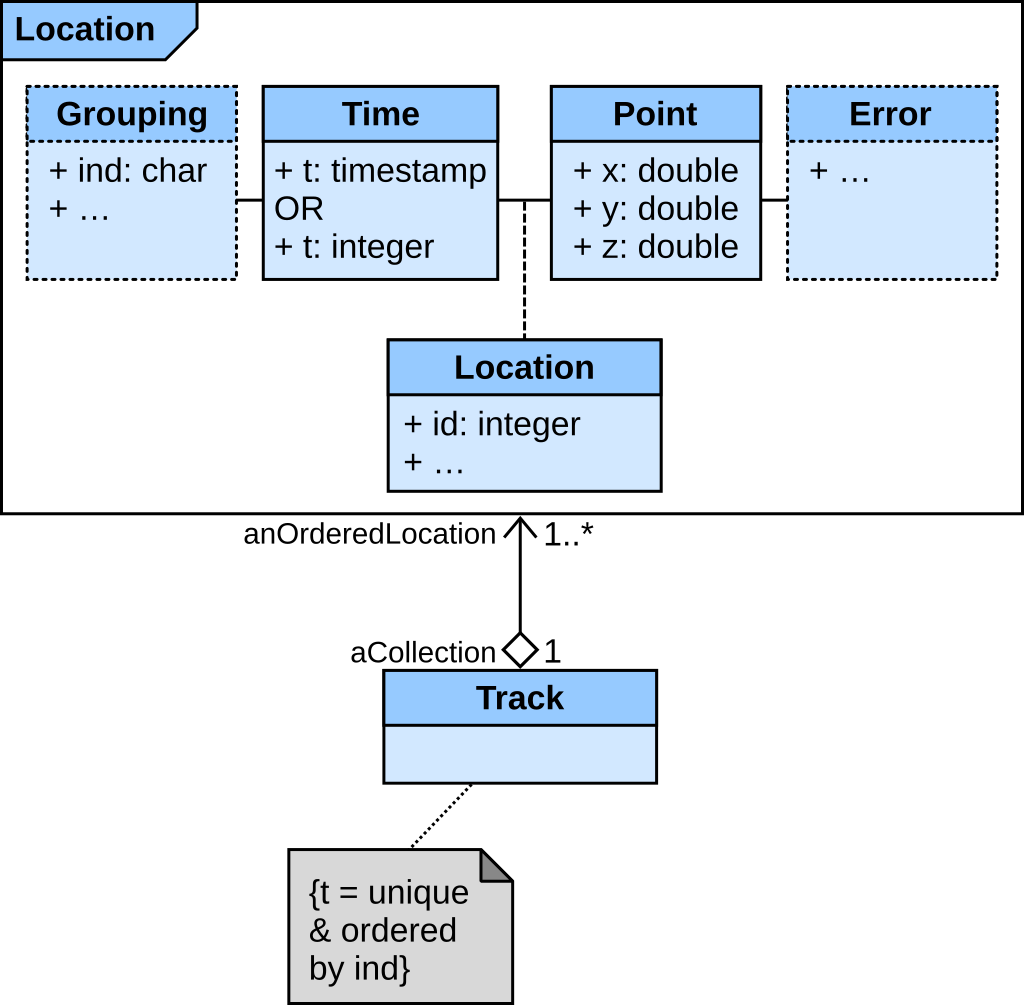
Tracking data, or a track, is a series of locations. This can be modeled as a collection of locations, unique and ordered in time by individual. As such, locations are the vertices of a single track object; conversely, all locations can be directly extracted from a single track (without any loss of information). The strong constraint on time is necessary and sufficient to organize the data in a track.
Steps
A step is specifically defined as the straight-line segment connecting two successive locations. In other words, it takes two and only two locations to define a step, with the constraints that they belong to the same grouping level (individual in its simplest form), and that the second location comes immediately after the first one.
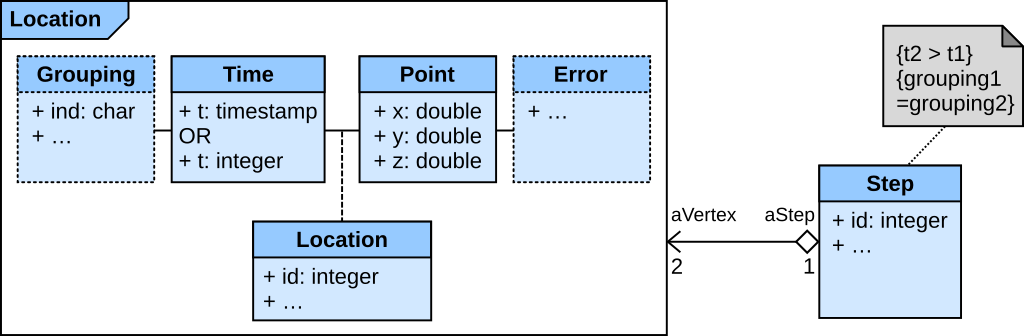
Note that a step can also include information at the level of the line segment. This can be for instance the amount of forest along the step, or the movement rate (i.e. speed).
Trajectories
Similarly to tracks, trajectories are defined by a series of steps. A trajectory is thus modeled as a collection of steps, unique and ordered in time by individual. As such, steps are the vertices of a single trajectory object; conversely, all steps can be directly extracted from a single trajectory (without any loss of information). The strong constraint on time is necessary and sufficient to organize the data in a trajectory.
Given the double equivalence between locations and tracks, on the one hand, and steps and trajectories, on the other hand, it follows that there is also a direct equivalence between a track and a trajectory (based on the same movement data); lossless conversion is possible in both directions.
What’s next?
The next step is to convert this conceptual model into R, using
classes that match the definitions provided here. With the package
sftraj, we propose an approach based on sf (for the spatial
components) to define central classes for movement. The only aim of
the package will be to present these central classes and basic
functions to build, handle, summarize and plot movement data. As a
matter of fact, this part of the work has already started, so we can
try things out… Stay tuned!
For the project team, Mathieu.
- Turchin, P. (1998). Quantitative analysis of movement: measuring and modeling population redistribution in animals and plants. Sinauer Associates, Sunderland, MA, USA. ^
- Martin, J., Tolon, V., Van Moorter, B., Basille, M., & Calenge, C. (2009). On the use of telemetry in habitat selection studies. In D. Barculo, & J. Daniels (Eds.), Telemetry: Research, Technology and Applications (pp. 37–55). Nova Science Publishers Inc. ^
- Roswell, C. (2011). Modeling of geographic information. Springer Handbook of Geographic Information, 3–6. https://doi.org/10.1007/978-3-540-72680-7_1 ^